|
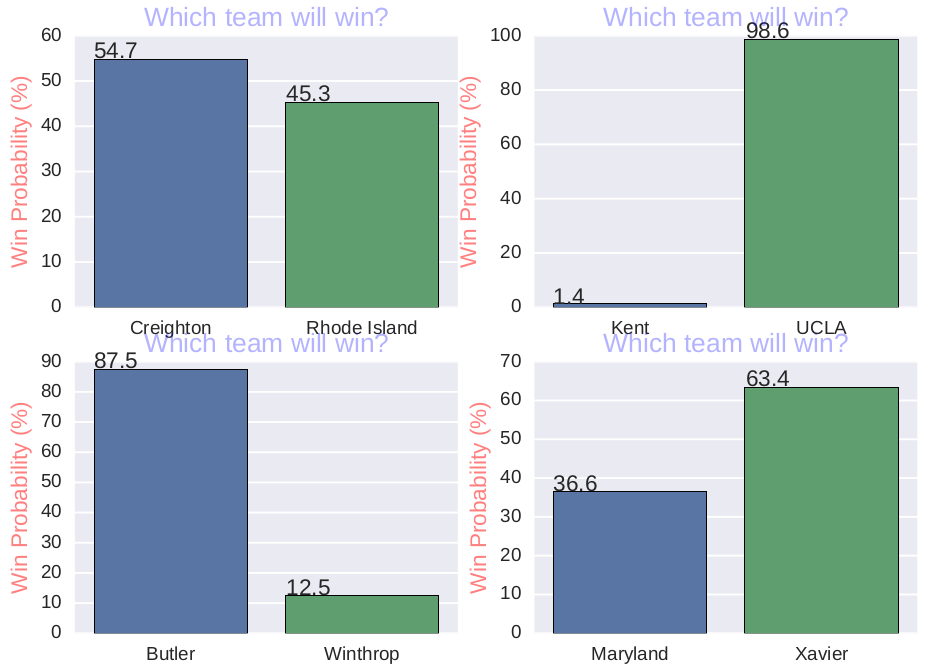
I mentioned in my previous blog entries how I used R and Python to generate predictions for previous NCAA basketball tournaments. For the upcoming tournament starting tomorrow, see "ncaa17.ipynb" for the IPython notebook and "ncaa17.py" at https://github.com/jk34/Kaggle_NCAA_logistic_trees_SVM for the Python script I used to generate the predictions for the upcoming 2017 tournament. The README.md file at the following link provides a report of how I conducted my analyses: https://github.com/jk34/Kaggle_NCAA_logistic_trees_SVM/blob/master/README.md I used getBPI.r to scrape the BPI rankings for each team. The predictions are in predictions.csv A few interesting predictions for the first round: -For the 1-16 and 2-15 seed matchups, most of the predictions predict the favorite to win with about 99% probability -11-seeded Xavier has a 64% chance to beat 6-seeded Maryland -6-seeded Creighton has only a 55% chance to beat 11-seeded Rhode Island -5-seeded Minnesota has only a 52% chance to beat 12-seeded Mid Tennessee -Other than the 8-9 seed matchups and 7-10 seed matchups, for the first round, the higher-seeded team is expected to win with probabilities around 60-90% Upsets are more likely to occur in the 2nd and 3rd rounds: -3-seeded Baylor and 6-seeded SMU is roughly a 50-50 game -1-seeded Villanova only has a 55% to beat each of 4-seeded Florida and 5-seeded Virginia -In fact, my predictions predict nearly an equal probability of winner of that bracket being either Villanova, Duke, Florida, or Virginia -7-seeded Saint Mary's has a 58% chance to upset 2-seeded Arizona. In the following round, it was a 55% chance to upset 3-seeded Florida State -1-seeded Gonzaga has only a 56% chance to beat 4-seeded West Virginia -1-seeded Kansas has only a 52% chance to beat 4-seeded Purdue -2-seeded Kentucky has only a 59% chance to beat 10-seeded Wichita State -3-seeded UCLA has only a 55% chance to beat 6-seeded Cincinnati Below are a few bar plots showing the probabilities of teams winning in their matchups:
0 Comments
For this project, I was interested in seeing which positions in NFL games have the highest correlation with the winning percentages of teams. I used the player ratings given by the Madden NFL video games for all the positions as the predictors, and the winning percentages of the teams for each player as the outcome variable for a Lasso regression model using R.
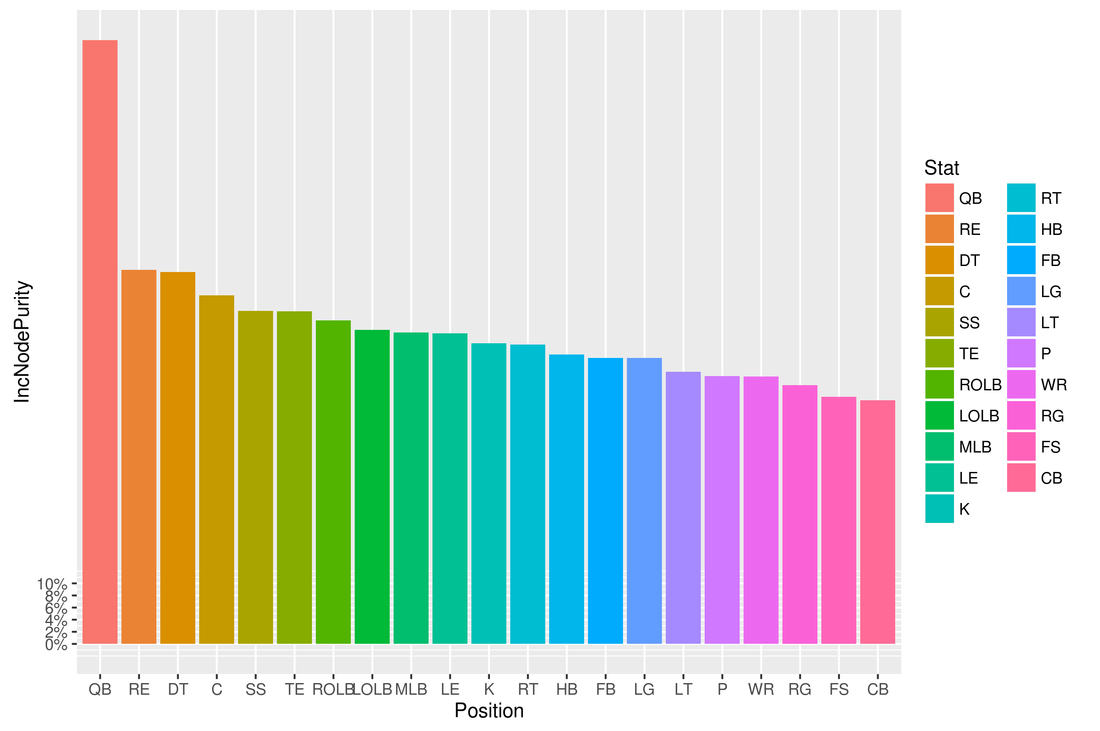
Before I could run the Lasso regression model, I had to obtain the data containing the ratings for each player, their positions, and the winning percentage of their team in a given season. I used the Python script maddenScrape.py to extract the Excel files containing the data from this website: http://maddenratings.weebly.com/madden-nfl-2003.html The Madden 2003-2005, 06-11 games contain the data for the 2002-2010 seasons in Excel files for each team in a season. These files contained the names for each team in the name of the file, but not in a column in the Excel file, so I had to use regular expressions to extract the team names and then create a new column in R containing the team names for each player, and then append that column to the dataframe containing the data in each Excel file. The Madden 13-16 games contain the data for the 2012-2015 seasons in just one Excel file for each season. These Excel files contained the teams for each player, so I did not need to use regular expressions. I had to do some more data cleaning. For example, most of the files contained the string "Buccaneers" for the Tampa Bay Buccaneers NFL team. However, some files contained the string "Bucs" instead, so I had to fix those problems. I then had dataframes for each season containing the team, name, position, and rating for each player. For example, for the 2002 season, the top few rows looked like this: Team LastName Position Overall 1 49ers Jeff McCurley C 58 2 49ers Jeremy Newberry C 84 3 49ers Anthony Parker CB 50 4 49ers Jimmy Williams CB 49 5 49ers Mike Rumph CB 67 6 49ers Rashad Holman CB 59 After I had dataframes for each season containing the team, name, position, and rating for each player, I had to prepare these dataframes for the Lasso regression model. However, I needed to make some assumptions in order to generate a relatively simple model. First, I had to assume that for most positions, only the ratings of the starters at each position affected the team's winning percentage. So for example, even though the San Francisco 49ers had 4 QBs on their roster for the 2002 season, I assumed that just one quarterback played all the plays at quarterback for every game that season, and that the other quarterbacks did not play at all. So I just used the highest rated QB and discarded all the other QBs. Similarly, I only kept 1 C, 2 CBs, 2 DT, 1 FB, 1 FS, 1 HB, 1 K, 1 LE, 1 LG, 1 LOLB, 1 LT, 1 MLB, 1 P, 1 QB, 1 RE, 1 RG, 1 ROLB, 1 RT, 1 SS, 1 TE, and 1 WRs for each team for each season in the dataframe. I then wanted to organize the dataframes for each season so that it contained the team and each position as the columns, with each entry of the dataframe containing the average rating for the top players for each team at each position. So for example, for the 2015 season, the first few rows of the new dataframe looked like: Team C CB DT FB FS HB K LE LG LOLB LT MLB P QB RE RG ROLB RT SS TE WR 1 49ers 79 79.5 79.0 88 81 78.50000 91 77 73 80 94 81.66667 51 81 82 88 89 72 91 84 87.0 2 Bears 84 82.5 71.0 82 75 83.00000 88 85 84 87 79 75.50000 73 79 69 88 79 74 81 90 85.5 3 Bengals 75 83.5 82.0 84 86 85.00000 76 88 84 74 95 80.00000 82 80 81 89 86 85 86 81 85.5 4 Bills 80 85.0 93.5 88 76 85.00000 89 90 71 83 86 71.00000 66 75 85 79 69 76 79 86 85.5 5 Broncos 70 92.0 74.0 80 85 80.50000 82 82 75 97 83 81.50000 76 92 84 86 83 79 87 82 91.0 6 Browns 89 87.0 77.5 63 89 73.33333 57 79 91 82 95 84.50000 89 72 79 86 88 77 90 76 85.0 Because I was interested in seeing in which positions the player ratings had a correlation with that player's team's winning percentage, and these Excel files did not contain the winning percentages of the team for each player, I had to obtain this data from ESPN using web scraping in R. There were some problems with this data as well that required data cleaning. For example, when I extracted the team names and winning percentages for the 2008 season, R extracted "z -Miami DolphinsMIA" as the team name for the Miami Dolphins. However, I was only interested in the string "Dolphins", so I had to use regular expressions to clean all the dirty data. After I cleaned the data, an example of what the dataframes containing the teams and their winning percentages for each season looked like: Team Winpct 1 Patriots 0.750 2 Bills 0.563 3 Dolphins 0.500 4 Jets 0.250 5 Steelers 0.688 6Bengals 0.656 For each season, I then merged the dataframe containing the ratings of the players at each position for each team with the dataframe containing each team and their winning percentage. I then merged these dataframes for each season into a final dataframe I then proceeded to run Lasso linear regression. I took a random sample of varying sizes in order to split up the data into training/validation, and test sets. I will now describe the results I obtained. When I used 4/5 of the data as the training/validation set with 10-fold cross-validation, and 1/5 of the data as the test set, I obtained R-squared=.0745, MSE=.0341. When I ran the model again using a different random sample of the same size for the training/validation and test sets, I obtained R-squared=.094 and MSE=.037, with coefficient values of 8.5e-06 for C, 3.63e-03 for QB, 5.02e-04 for RE, 8.24e-04 for TE, and zeros for the other positions. Using 1/5 of the data as the test test, and 5-fold cross-validation, I obtained R-squared=.11, MSE=.029 with coefficients of 2.846 for C, -1.06e-04 for LT, 4.08e-03 for QB, 1.12e-03 for RE, 5.51e-04 for RT, 8.99e-04 for SS, 1.30e-03 for TE, and zeros for the other positions. I then used Random Forest in R. For 500 trees, I obtained R-squared=.009 and MSE=.032. The variable importance plot showing the value of IncNodePurity for each position is displayed in the "importance500trees.png" file. For 1000 trees, I obtained R-squared=.0026 and MSE=.033. The variable importance plot showing the value of IncNodePurity for each position is displayed at the bottom of this post. Judging by the variable importance plots generated from Random Forest, along with the non-zero coefficients from the Lasso regression, it seems that QB, RE, TE, and SS are the positions in which the player rating has the highest correlation with a team's winning percentage. While casual observers would agree that QB is the most important position in the game of football, I believe casual observers would disagree with the findings of my analysis which shows that TE, RE, and SS are also the most important positions. Casual observers would probably believe that WR, CB, and LT are the next most important positions after QB The R and Python code I used for this project is located at: https://github.com/jk34/NFL_model In this post, I will talk about how I used Natural Language Processing in Python to determine whether an internet forum has an overall positive or negative tone. I determined the most common words and bigrams in the posts of the users
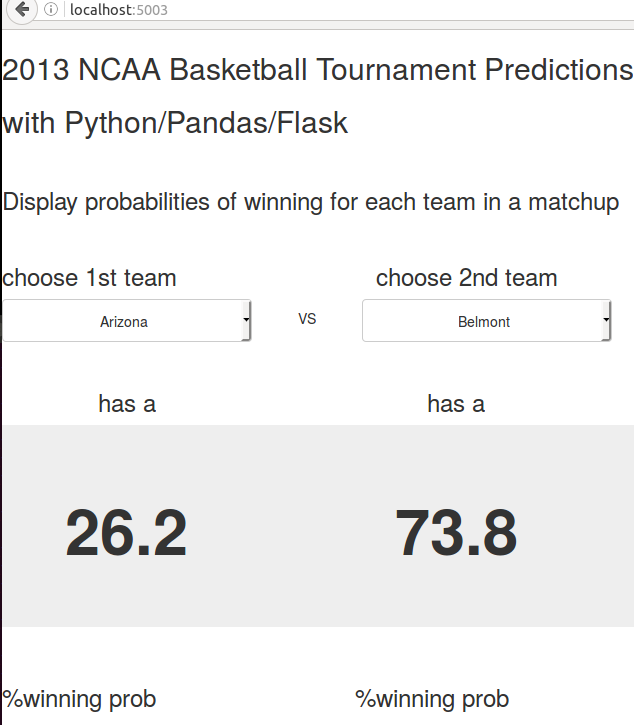
I created a simple web application using Flask along with HTML/CSS/Javascript that allows the user to choose 2 teams that participated in the 2013 NCAA Basketball Tournament and displays the probability of each team winning in that matchup. The training set data and machine learning algorithms used to generate the predictions was explained in this blog post: http://jerrykim.weebly.com/blog/using-pandas-on-ncaa-tournament-data-from-kaggle Details for the code used to generate this web application at: https://github.com/jk34/NCAA_Flask
The online version of my resume can be viewed at http://jerrykim.herokuapp.com/
I completed this project as part of the Udacity course "Javascript Basics": https://www.udacity.com/course/javascript-basics--ud804 I used some of the code from here: https://github.com/lei-clearsky/nanodegree-fewd-p2 I created a web application using Flask. It is based on this tutorial: pythonprogramming.net
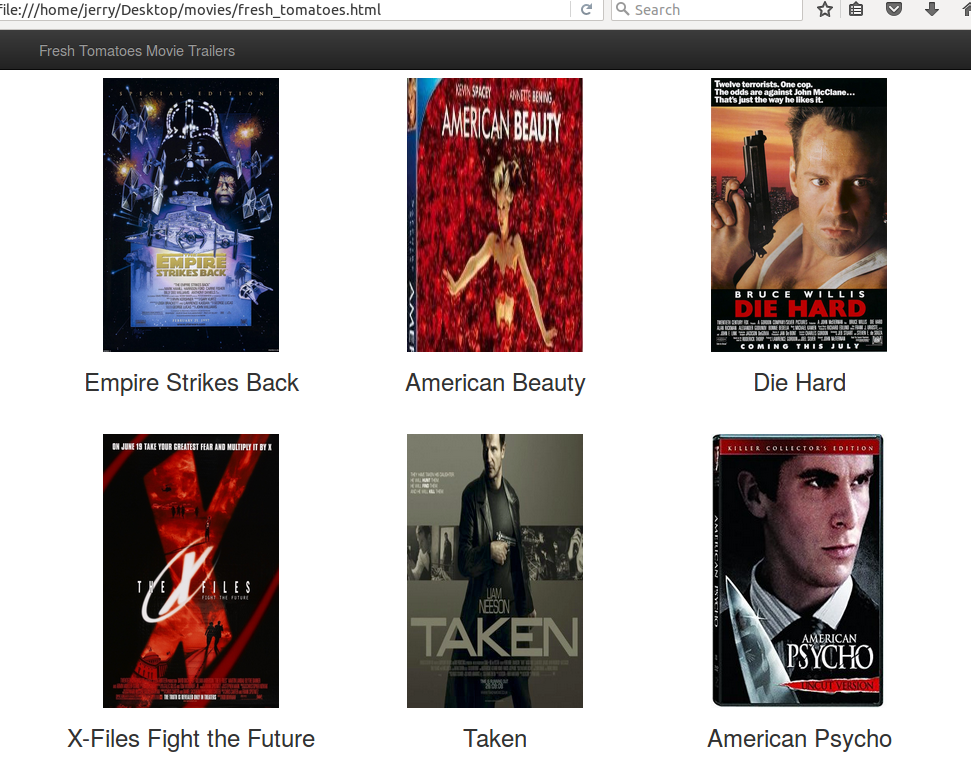
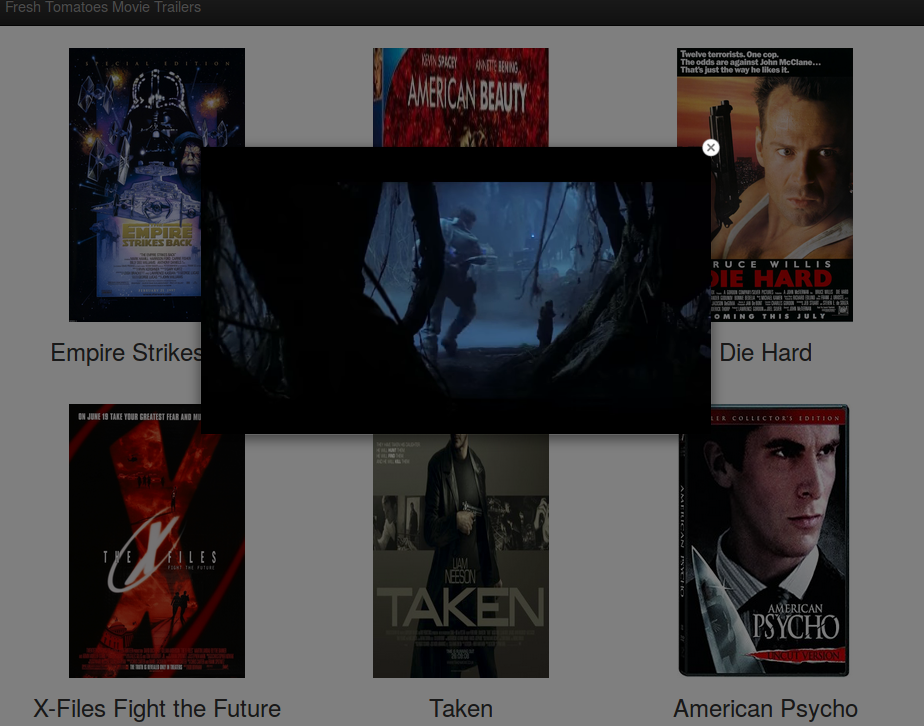
This application lets the user signup and register with their username, email, and password. Then, the user can log in or log out. There are also links to my Github and Linkedin pages at the top bar of the webpage. Clicking on the "Interactive" link lets the user guess my name and enter the value. I created a blog web application using Flask. It is based on this tutorial: http://charlesleifer.com/blog/how-to-make-a-flask-blog-in-one-hour-or-less/ I implemented a feature that lets the user add an image to the content of their blog entry by utilizing functions from this link: http://code.runnable.com/UiPcaBXaxGNYAAAL/how-to-upload-a-file-to-the-server-in-flask-for-python I also modified the HTML contents of the blog and added the links to my Github and Linkedin pages at the top bar of the webpage Below is a screenshot of what it should look like when you run this blog application in your browser using Flask: The code I used to create this application is located at: https://github.com/jk34/Blog_Flask The guide to run this application is at: http://charlesleifer.com/blog/how-to-make-a-flask-blog-in-one-hour-or-less/ I just completed a project for the Udacity course "Programming Foundations with Python". The project involved creating a website that shows a few movies and allows the user to view the movie trailer of whatever movie he/she is interested in. Screenshots are below: The user then can see a trailer for "Empire Strikes Back" if he clicks on it The code for this can be viewed at github.com/jk34/MovieTrailer In this blog post I will discuss my updated work on the San Francisco Crime Classification competition by Kaggle. The data and description of the competition is located at: https://www.kaggle.com/c/sf-crime
I had used Linear Discriminant Analysis and Random Forest. I have now been able to run Boosting and obtained much better log-loss scores First of all, I was able to generate the new features "Intersection" and "Night", utilize the data.table package to read in large csv faster, and make use of sparse matrices to save memory from this link: https://brittlab.uwaterloo.ca/2015/11/01/KaggleSFcrime/ I then implemented Gradient Boosting by using the "caret" and "xgboost" packages. I first tried eta=.3 (the larger eta is, the smaller the regularization penalty term is). With Cross-Validation using 3 folds, I found that the 16th iteration produced the smallest logloss.mean value of 2.56. However, my previous submission to Kaggle using LDA produced a log-loss of around 2.58. Because the validation error is smaller than what the test error would be, I knew that this 2.56 value was unacceptable. I then guessed that perhaps the previous LDA model overfitted the training set, so I tried increasing the regularization penalty term and decreased eta to 0.1 According to the xgboost documentation page, if you decrease eta, you must increase the number of boosting iterations. I thus tried 50 iterations. I then submitted this to Kaggle, and my logloss score was 2.43! That was much better than the 2.58 I got from LDA I should also note that I tried to use the parameter tuning with "caret". However, it was running too slow on my machine. Just trying a 2-fold CV, with 40 max iterations on 3 different eta values ran for over 8 hours! In addition to Boosting, I also tried to use Random Forests, use the bigRF package, and Neural Networks. In my previous analysis using Random Forests, I kept running into errors due to my computer not having enough memory. I recently purchased a new laptop with more RAM, but I have gotten those same errors with not sufficient memory when running Random Forests. I also could not get the bigRF package to work. I believe it was because it doesn't work on my version of R. As for Neural Networks, I am working on that as I type this post You can find the code I used for this analysis at: https://github.com/jk34/Kaggle_SF_Crime_Classification/blob/master/run_improved.r I have updated my work on the data set provided by Kaggle on the NCAA competition. To reiterate, the data is provided at: https://www.kaggle.com/c/march-machine-learning-mania-2015
I also utilized the blog_utility.r script from https://statsguys.wordpress.com/2014/03/15/data-analytics-for-beginners-march-machine-learning-mania-part-ii/ In this post, I converted the R code provided in the link above into Python code with Pandas. I will briefly discuss how the code works: 1st step: Look at all games from the tournament for a given season (training set should contain multiple seasons) by reading in tourneyRes=pd.read_csv("tourney_compact_results.csv"). Then we loop through each row of that dataframe and we concatenate the season “seasonletter” with the teamID for the winning team (wteam in tourneyRes) and the teamID of the losing team (lteam in tourneyRes). We place these newly formed strings into a new data frame model_data_frame with the results model_data_frame now contains “matchup” (ex. 1234_5678), which is a Pandas Series concatenated with “result/Win” Pandas series (contains 0’s and 1’s, depending on the below) ixs = season_matches['wteam'] < season_matches['lteam'] Then, we create a new dataframe df2 that splits “matchup” (for example, 2008_1234_5678) and stores the teamIDs into HomeID and AwayID. Then we JOIN these columns onto model_data_frame 2nd step: Use teamMetrics =team_metrics_by_season(seasonletter) function to read in tourney_seeds.csv, which contains teamID, BPI, and SEED values for each team that made the tournament in a given season. Then we look through the entire results for a given regular season (the season according to “seasonletter”), which we obtain from regular_season_compact_results.csv. We then keep track of the number of wins and losses, and then compute the number of wins divided by total number of games (TWPCT) for each tournament team in a given regular season. “teamMetrics” now has the columns set as team_metrics.columns = ['TEAMID', 'A_TWPCT', 'A_SEED','A_BPI'] 3rd step: Then we MERGE model_data_frame (containing HomeID, AwayID, and Results of 0’s and 1’s for the tournament) with teamMetrics (containing TEAMID, TWPCT, SEED, BPI based on regular season data) ON HomeID=TEAMID. Then do the same for AwayID Resulting training set looks like: head(trainData) Matchup Win HomeID AwayID A_TWPCT A_SEED A_BPI B_TWPCT B_SEED B_BPI 12 2008_1164_1291 0 1164 1291 0.412 16 288 0.562 16 163 4th Step: The test Set is similar to above, except we first start off by reading in all the teams and their seeds for a particular season tourneySeeds= pd.read_csv("tourney_seeds.csv", sep=',') playoffTeams = season_seeds['team'] playoffTeams = playoffTeams.sort_values(ascending=[1]) Then, assign create a Pandas Series containing matchups of every possible matchup of teams in a particular tournament idcol = pd.Series(str_seasonletter+ "_" + "_".join([str(a),str(b)]) for a,b in combinations(playoffTeams,2)) form = idcol.to_frame() form.columns=['Matchup'] form['result'] = np.NaN Assign NaN to every matchup because we don’t know yet the results for a test set. The resulting test set looks identical to the training set, except the “Win” column is all NA values In addition to Logistic Regression, I also tried to utilize Neural Networks to generate predictions of which team would win in a potential matchup. However, I could not get the code to work. I will attempt to fix this in the near future The Python script is the "ncaa.py" file at https://github.com/jk34/Kaggle_NCAA_logistic_trees_SVM, which provides all the data and code I used LINEAR DISCRIMINANT ANALYSIS (LDA) I also used LDA in the R code ( the updated "ncaa.r" file in my Github page). I obtained a logloss score of .631 (when using just BPI, SEED, and TWPCT as features). This is better than the .65 values I got from Logistic Regression and Random Forest |
AuthorHello world, my name is Jerry Kim. I have a Master's Degree in Physics and years of work experience in Image Processing, Machine Learning, and Deep Learning. I mostly have used C++, Matlab, and Python. I created this website to showcase a small sample of the things that I have worked on Archives
March 2017
Categories |


 RSS Feed
RSS Feed
