|
For this project, I was interested in seeing which positions in NFL games have the highest correlation with the winning percentages of teams. I used the player ratings given by the Madden NFL video games for all the positions as the predictors, and the winning percentages of the teams for each player as the outcome variable for a Lasso regression model using R.
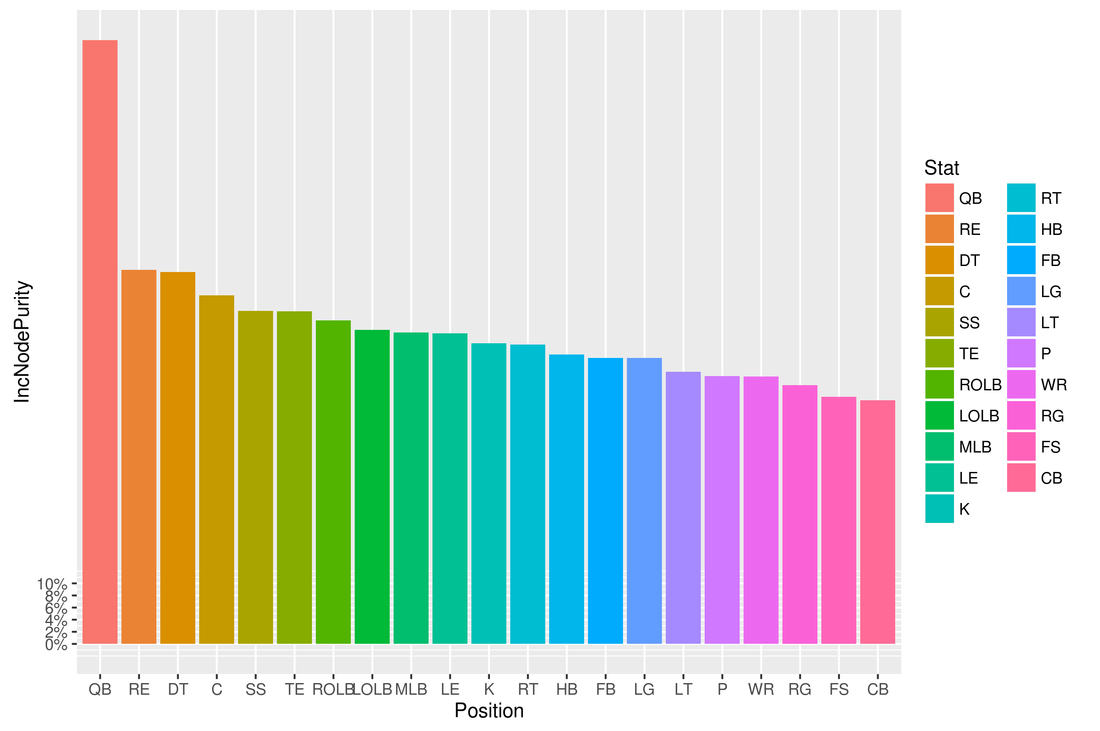
Before I could run the Lasso regression model, I had to obtain the data containing the ratings for each player, their positions, and the winning percentage of their team in a given season. I used the Python script maddenScrape.py to extract the Excel files containing the data from this website: http://maddenratings.weebly.com/madden-nfl-2003.html The Madden 2003-2005, 06-11 games contain the data for the 2002-2010 seasons in Excel files for each team in a season. These files contained the names for each team in the name of the file, but not in a column in the Excel file, so I had to use regular expressions to extract the team names and then create a new column in R containing the team names for each player, and then append that column to the dataframe containing the data in each Excel file. The Madden 13-16 games contain the data for the 2012-2015 seasons in just one Excel file for each season. These Excel files contained the teams for each player, so I did not need to use regular expressions. I had to do some more data cleaning. For example, most of the files contained the string "Buccaneers" for the Tampa Bay Buccaneers NFL team. However, some files contained the string "Bucs" instead, so I had to fix those problems. I then had dataframes for each season containing the team, name, position, and rating for each player. For example, for the 2002 season, the top few rows looked like this: Team LastName Position Overall 1 49ers Jeff McCurley C 58 2 49ers Jeremy Newberry C 84 3 49ers Anthony Parker CB 50 4 49ers Jimmy Williams CB 49 5 49ers Mike Rumph CB 67 6 49ers Rashad Holman CB 59 After I had dataframes for each season containing the team, name, position, and rating for each player, I had to prepare these dataframes for the Lasso regression model. However, I needed to make some assumptions in order to generate a relatively simple model. First, I had to assume that for most positions, only the ratings of the starters at each position affected the team's winning percentage. So for example, even though the San Francisco 49ers had 4 QBs on their roster for the 2002 season, I assumed that just one quarterback played all the plays at quarterback for every game that season, and that the other quarterbacks did not play at all. So I just used the highest rated QB and discarded all the other QBs. Similarly, I only kept 1 C, 2 CBs, 2 DT, 1 FB, 1 FS, 1 HB, 1 K, 1 LE, 1 LG, 1 LOLB, 1 LT, 1 MLB, 1 P, 1 QB, 1 RE, 1 RG, 1 ROLB, 1 RT, 1 SS, 1 TE, and 1 WRs for each team for each season in the dataframe. I then wanted to organize the dataframes for each season so that it contained the team and each position as the columns, with each entry of the dataframe containing the average rating for the top players for each team at each position. So for example, for the 2015 season, the first few rows of the new dataframe looked like: Team C CB DT FB FS HB K LE LG LOLB LT MLB P QB RE RG ROLB RT SS TE WR 1 49ers 79 79.5 79.0 88 81 78.50000 91 77 73 80 94 81.66667 51 81 82 88 89 72 91 84 87.0 2 Bears 84 82.5 71.0 82 75 83.00000 88 85 84 87 79 75.50000 73 79 69 88 79 74 81 90 85.5 3 Bengals 75 83.5 82.0 84 86 85.00000 76 88 84 74 95 80.00000 82 80 81 89 86 85 86 81 85.5 4 Bills 80 85.0 93.5 88 76 85.00000 89 90 71 83 86 71.00000 66 75 85 79 69 76 79 86 85.5 5 Broncos 70 92.0 74.0 80 85 80.50000 82 82 75 97 83 81.50000 76 92 84 86 83 79 87 82 91.0 6 Browns 89 87.0 77.5 63 89 73.33333 57 79 91 82 95 84.50000 89 72 79 86 88 77 90 76 85.0 Because I was interested in seeing in which positions the player ratings had a correlation with that player's team's winning percentage, and these Excel files did not contain the winning percentages of the team for each player, I had to obtain this data from ESPN using web scraping in R. There were some problems with this data as well that required data cleaning. For example, when I extracted the team names and winning percentages for the 2008 season, R extracted "z -Miami DolphinsMIA" as the team name for the Miami Dolphins. However, I was only interested in the string "Dolphins", so I had to use regular expressions to clean all the dirty data. After I cleaned the data, an example of what the dataframes containing the teams and their winning percentages for each season looked like: Team Winpct 1 Patriots 0.750 2 Bills 0.563 3 Dolphins 0.500 4 Jets 0.250 5 Steelers 0.688 6Bengals 0.656 For each season, I then merged the dataframe containing the ratings of the players at each position for each team with the dataframe containing each team and their winning percentage. I then merged these dataframes for each season into a final dataframe I then proceeded to run Lasso linear regression. I took a random sample of varying sizes in order to split up the data into training/validation, and test sets. I will now describe the results I obtained. When I used 4/5 of the data as the training/validation set with 10-fold cross-validation, and 1/5 of the data as the test set, I obtained R-squared=.0745, MSE=.0341. When I ran the model again using a different random sample of the same size for the training/validation and test sets, I obtained R-squared=.094 and MSE=.037, with coefficient values of 8.5e-06 for C, 3.63e-03 for QB, 5.02e-04 for RE, 8.24e-04 for TE, and zeros for the other positions. Using 1/5 of the data as the test test, and 5-fold cross-validation, I obtained R-squared=.11, MSE=.029 with coefficients of 2.846 for C, -1.06e-04 for LT, 4.08e-03 for QB, 1.12e-03 for RE, 5.51e-04 for RT, 8.99e-04 for SS, 1.30e-03 for TE, and zeros for the other positions. I then used Random Forest in R. For 500 trees, I obtained R-squared=.009 and MSE=.032. The variable importance plot showing the value of IncNodePurity for each position is displayed in the "importance500trees.png" file. For 1000 trees, I obtained R-squared=.0026 and MSE=.033. The variable importance plot showing the value of IncNodePurity for each position is displayed at the bottom of this post. Judging by the variable importance plots generated from Random Forest, along with the non-zero coefficients from the Lasso regression, it seems that QB, RE, TE, and SS are the positions in which the player rating has the highest correlation with a team's winning percentage. While casual observers would agree that QB is the most important position in the game of football, I believe casual observers would disagree with the findings of my analysis which shows that TE, RE, and SS are also the most important positions. Casual observers would probably believe that WR, CB, and LT are the next most important positions after QB The R and Python code I used for this project is located at: https://github.com/jk34/NFL_model
0 Comments
|
AuthorHello world, my name is Jerry Kim. I have a Master's Degree in Physics and years of work experience in Image Processing, Machine Learning, and Deep Learning. I mostly have used C++, Matlab, and Python. I created this website to showcase a small sample of the things that I have worked on Archives
March 2017
Categories |
 RSS Feed
RSS Feed
